(A)次に入る言葉を答えなさい。
企業は( あ )の増減に対して原価の発生がどのよ うに変化するかについて知ることで、将来の原価の発生額を予測することが可能になります。そのために、原価を変動費と固定費に分解することが必要となり、これを原価の 固変分解といいます。
この固変分解は一般的には、IE法 (技術的予測法)と過去の実績データにもとづく方法に分類され、さらに後者は、( い )、( う )、高低点法、回帰分析法(最小自乗法)に分類されます。
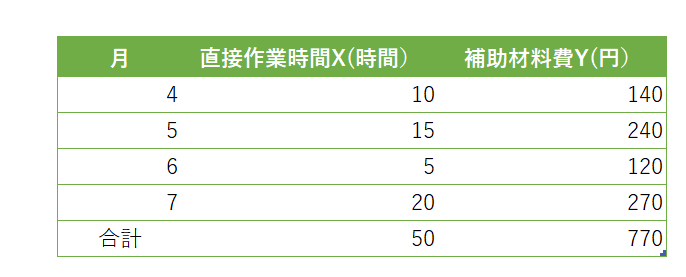
(B)直接作業時間(X)と補助材料費(Y)に関する過去4カ月間の実績データは下記であった。これらはすべて正常範囲内のデータである。補助材料費の原価線は、Y=aX+bで表せるも のとして、(1)高低点法と、(2)最小自乗法によってa(変動費率)とb(固定費)を計算しなさい。
(A)
あ ⇒ 生産量や販売量
い ⇒ 費目別精査法
う ⇒ スキャッター・チャート法
(B)
(1)高低点法 a(変動費率)= 10 、b(固定費)= 70
(2)最小自乗法 a(変動費率)= 11 、b(固定費)= 55
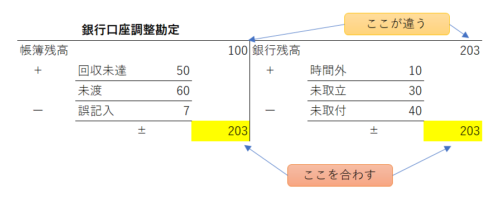
高低点法による固変分解とは
高低点法とは過去の実績データのうち、その費目の最高の営業量のときの実績データと最低の営業量のときの実績データから、原価の推移を直線とみなし、変動費と固定費とに分解する方法です。(金額の最高と最低ではなく、営業量の最高と最低を選ぶところがポイントです)

上の例題だと次の形となります。
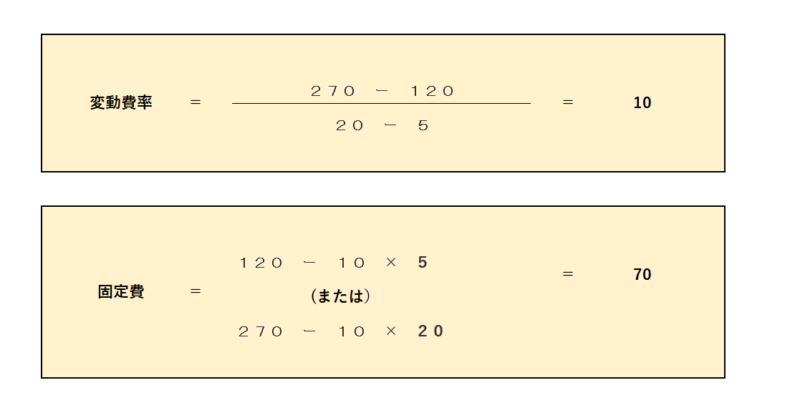
最小自乗法による固変分解とは
最小自乗法とは、原価の推移を営業量の変化に関係づけられる直線と定義して、原価の実績データの平均線を方程式を立てて求め、その連立方程式を解くことにより変動費と固定費に分解する方法です。
具体的には次の2つの方程式を解きます。
Y:原価発生額、X:営業量、 a:変動費率、b:固定費、n:データ数、 Σ:合計 として
① ΣY = a Σ X + nb
② Σ XY = aΣX2 + b Σ X
上の例だと、まず下の表を作り、準備します。
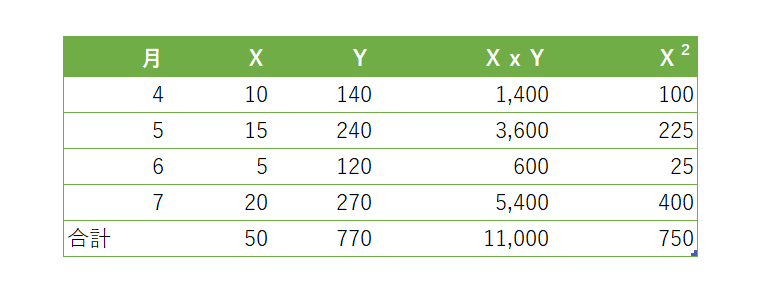
表から方程式を作ると
①770 = 50a + 4b
②11,000 = 750a + 50b
この式を解くと、
①770 = 50a+4b
②11000 = 750a+50b
▼①を整理する
-50a-4b = -770
▼②を整理する
-750a-50b = -11000
▼aの係数を揃える
①×15 → -750a-60b = -11550
②×1 → -750a-50b = -11000
▼式を引いてbを求める-750a -60b = -11550
-) -750a -50b = -11000
-10b = -550
b = 55
▼整理した①にbの値を代入する
-50a-(4×55) = -770
-50a-220 = -770
-50a = -770+220
-50a = -550
a = 11
▼解
a = 11 b = 55
となります。
一見難しそうですが、ポイントは
① 原価線は、Y=aX+b で表現され
②各期間の Y=aX+b を合計する
③②の式の両辺にXをかける
④②③の式を解く
です。